Chemical equation can be used to determine mass relationships between reactants and products. There are two methods that can be followed. One is very math oriented and used in the text. The other is more natural and intuitive proportional method. I will describe the proportional method first.

The proportional or mass based method.

Burning carbon and carbon containing compounds in air can produce carbon monoxide. This is one reason why carbon monoxide detectors are marketed for consumers. Space heaters have sometimes killed unsuspecting people. What they didn't know did hurt them. Carbon monoxide is poisonous. It is cumulative and even if it doesn't kill it can cause chronic illness and brain damage.

The equation says that two moles of carbon react exactly with one mole of oxygen. The coefficients in the balanced equation tell the moles of each substance involved in the equation.

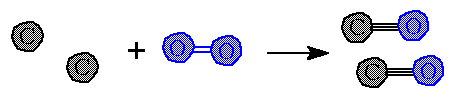
This mole level of the equation can be converted to masses. The molar masses for each reactant and product are introduced and the moles can be converted to masses (grams)

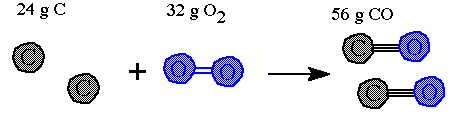
Notice that the total mass of reactants equals the total mass for of products. This shows the law of conservation of mass at work.

These numbers show what masses are needed to match the balanced equation molar amounts of reactants and products.

Example:

What will happen if the amount of carbon was divided in half?

The masses involved would all be cut in half. The values below show that all the mases would be one half the original.

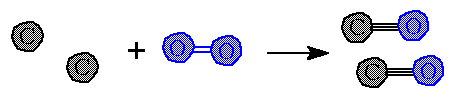
Example: If you want to know how many grams of oxygen will react with 1 gram of carbon you can divide every thing by 12 to get "1" gram of carbon. The other masses must also be divided by 12. Because this is an equation. The multiples used on one term must be used on all.

Masses can be scaled up or down. If you want to deal with larger quantities, multiply by the required number.

Example: What would happen if you wanted to burn 1200 grams of carbon? How many grams of oxygen would be needed? How many grams of CO would be made?

Answer:

Step 1. Establish the masses needed for the balanced equation.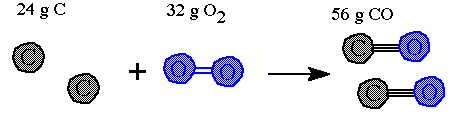

Step 2. Write in the masses given in the question.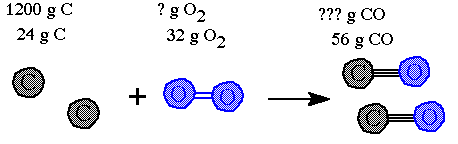

Step 3. Decide on a number that needs to be used to scale up the 24 grams C to the 1200 grams. You do this by dividing the 1200 by the 24. The answer is "50" this means everything in the equation needs to be "scaled up" by a multiple of "50".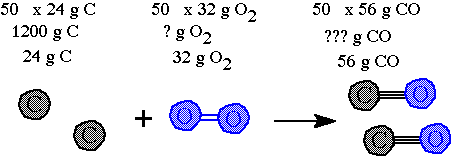

Step 4. Multiply out the terms

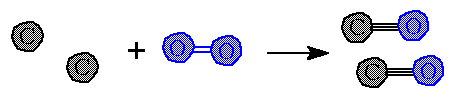
Example: What would happen if you wanted to react 450 grams of nitrogen with hydrogen? How many grams of hydrogen would be needed? How many grams of NH₃ would be made?

The reaction is N₂(g) + 3 H₂(g)---> 2 NH₃(g)

Answer:

Step 1. Identify the molar masses for each compound.

1 mole N₂ = 28 grams N₂ ; 1 mole H₂ = 2 grams H₂; 1 mole NH₃ = 17 grams NH₃

Establish the moles needed for the balanced equation.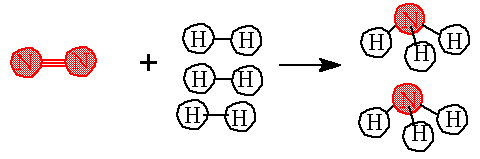

Step 2 Write in the molar amounts for the equation.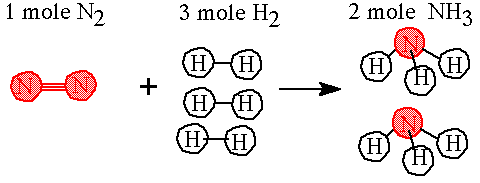

Step 3. Determine the required masses by writing in the molar masses.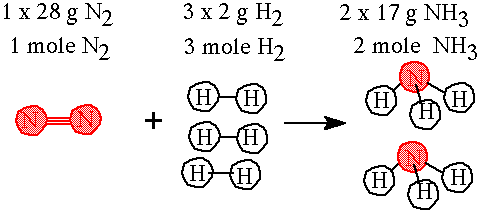

Step 4. Decide on a number that needs to be used to scale up the 28 grams of nitrogen to the 450 grams available. You do this by dividing the 450 by the 28. The answer is "16.07" this means everything in the equation needs to be "scaled up" by a multiple of 16.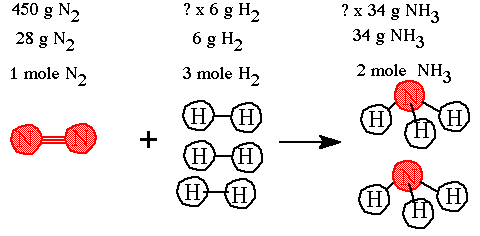

Step 5. Multiply out the terms by the multiple 16.07 and round off to the correct sf.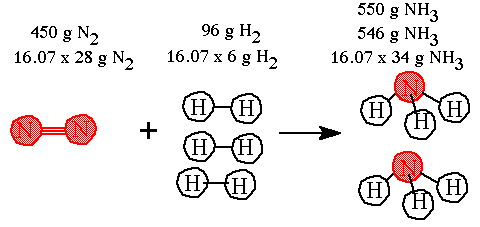

 The 450 grams of nitrogen requires 96 grams of hydrogen and the reaction will produce 85% grams of ammonia. (These numbers are to two sf)