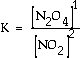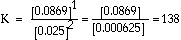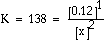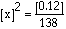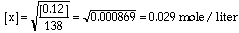|
Reactions Irreversible and Reversible Equilibrium Equations and Equilibrium Constants |
Online Introductory Chemistry |
Irreversible reactions
that go to completion: Explosions are nonreversible reactions and to go to completion. There is no going back to reactants. After the reaction occurs
the reaction mixture contains only products plus any left over excess
reactants. The products do not break down to reform reactants. Burning
an organic compound like methane, CH4, is an example of a
reaction that goes to completion. When you burn natural gas in air with enough O2 the
products are CO2 and H2O. The methane is completely
converted to these products. Extra oxygen in the atmosphere is still
around, but it isn't part of a reversible process. The CO2 , carbon dioxide, and H2O , water, do not react to form CH4 and oxygen. CH4 + O2 ------> CO2 + 2 H2O not reversible If we tried to describe the condition of reactants and products with an equilibrium
constant, the K eq would have a value of infinity. The K is large because reactants are basically zero and products dominate the mixture. In fact, there
are no reactant methane molecules left. The
larger the value for the equilibrium constant the more the reaction
goes to completion. Irreversible reactions can be thought to
have an infinite equilibrium constant so there are no reactants
left. What does
an equilibrium constant tell: In an equilibrium mixture both reactants
and products coexist. The values
for equilibrium constants are tied to the amounts of reactants and products
in equilibrium mixtures. The number values for "K" are determined by experiments
measuring equilibrium concentrations. The "K" tells the equilibrium
ratio of products to reactants. The value for
K is large when products dominate the mixture. This implies that products are 'favored' over reactants. When the value for
K is small the reactants dominate the mixture and are 'favored' over products. Large
K > 1 products are "favored" they dominate the mixture K
= 1 neither reactants nor products are favored Small
K < 1 reactants are "favored" they dominate the mixture The term "favored"
means that side of the equation has higher numbers of moles and higher
concentrations than the other. A large
K is more than '1' and can be huge, 1 x 1034 K
= 1 neither reactants nor products are favored A small
K is less than 1 and can be tiny, 4 x 10-41
Reversible
reactions have similar mechanical examples. Image a pair of
identical water filled fish tanks connected by a tube with a sliding "gate".
One tank has no fish and the other contains 10 identical fish.
Predict what will happen when you open the gate that blocks
access to the empty tank. Hmm! I hope
we agree. The fish will swim around and the 10 fish will eventually
distribute themselves between the two tanks. The "equilibrium"
condition will have 5 fish in each tank. If you took pictures
of the process as the fish swim around they might look like
these. This animation illustrates what will happen as the fish move to establish equilibrium. The fish
population will reach an equilibrium with five fish in each
tank. The ratio of the number of fish in the right hand side
to the number in the left hand side will be "1". The value for
the equilibrium constant is a "1". Neither side is favored. Now suppose
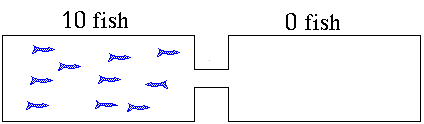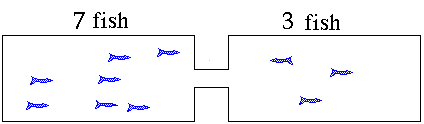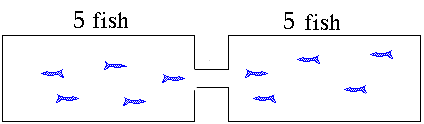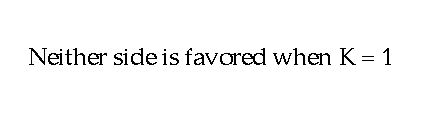
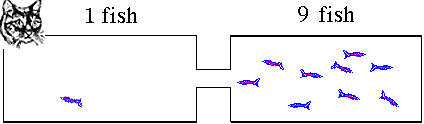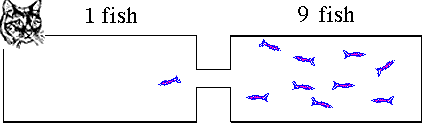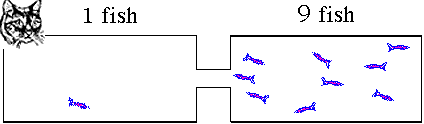
for a new equilibrium condition that the right hand tank was very attractive. The cat makes one side less attractive to the fish. Suppose 9 fish on average
stay in the right hand tank leaving only one fish in the reactants
or left hand side. The ratio of products to reactants will be
ratio = 9/1 = 9. The right hand tank is favored. Products will
dominate. The value for K is greater than 1. Reversible
chemical reactions follow a similar pattern. At equilibrium
the number of reactant and product molecules stay constant.
The identity of individual molecules keeps changing . The reactants
are initially the only molecules around. They react to form
products. The amount of reactant dwindles and the forward reaction
slows down. The product amount increases at the same time the
reactants are disappearing. The products "break down" to form
reactants. The rate for this reverse reaction increases as the
amount of product grows. Ultimately there comes a time when
the forward reaction rate and the reverse reaction rate are
equal. The mixture is at equilibrium. How to use balanced equations
to determine equilibrium expressions:
How the equilibrium
expression is determined The entries are
gas pressures for gases and concentrations in moles per liter for dissolved
substances. The never
includes pure solids or pure liquids. These have fixed values and are
not a factor in equilibrium changes. Example: The reversible reaction
2 H2(g) + N2(g) has an equilibrium
expression that looks like this. The brackets are a shorthand code for
concentration in units of moles per liter. Notice the exponents
are "1" on the nitrogen, N2, and hydrazine, N2H4.
The exponent is a "2" on the hydrogen, H2. The exponents
are the same as the coefficients in the balanced equation.
Equilibrium expressions
are written as a fraction. The activities of products appear in the numerator
and the activities of reactants in the denominator. The "activities" are
a measure of how much reaction potential a substance has. For gases activity
depends on pressure. For dissolved substances activity depends on concentration.

![]() N2H4(g)
N2H4(g)
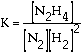
Exercise For the equilibrium equation here, what is the equilibrium expression? N2 (g) + 3 H2
(g) Answer: This is
the accepted equilibrium expression. Normally
heat is not included, but literally it can appear in the expression
with the appropriate part of the equation. Here for an exothermic
reaction a HEAT term can be placed with products, in the numerator. Exercise What is the equilibrium
expression for the following reaction? N2(g) + 2 O2(g)
Answer: This is
the accepted equilibrium expression. Normally
heat is not included, but literally it can appear in the expression
with the appropriate part of the equation. Here for an exothermic
reaction a HEAT term can be placed with products, in the numerator. Exercise What is the equilibrium
expression for the following reaction? CaCl2(s) Answer: This is
the accepted equilibrium expression. The reactant CaCl2(s)
does not appear in the expression because it is a "pure" solid.
All solids are assumed to be pure. Normally
the "1" in the
denominator is omitted. The expression is simplified.
![]() 2 NH3(g) + heat
2 NH3(g) + heat
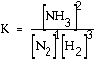
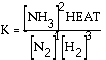
![]() 2
NO2(g) + heat
2
NO2(g) + heat
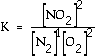
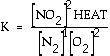
![]() Ca2+(aq) + 2 Cl-(aq)
Ca2+(aq) + 2 Cl-(aq)
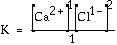
|
How to use equilibrium concentrations to determine equilibrium constants: |
|
Exercise |
|
a. What is the equilibrium constant for the following reaction?
|
|
Answer: |
|||||||||||
|
|
Online Introductory Chemistry |
|
|
|
|