Definition of pH, pOH, "p", sample calculations
Definition of pH, pOH, "p", sample calculations
General The acid potential of aqueous solutions is measured in terms of the pH scale. The symbol "p" means take the negative logarithm of whatever follows in the formula. for pH, pOH, p[anything] . The pH scale is intended to be a convenience. Tremendous swings in hydrogen ion (hydronium ion) concentration occur in water when acids or bases are mixed with water. These changes can be as big as 1 x 1014, This means concentrations can change by multiples as big as one hundred trillion, 100,000,000,000,000. The pH scale is a logarithmic scale. Every multiple of ten in H1+ concentration equals one unit on the logarithm scale. Physically the pH is intended to tell what the acid "potential" is for a solution. In a sense the system is INVERTED so a low pH value indicates a great acid potential while a high pH indicates a low acid potential. ( Sad but true this is upside down and counter intuitive.) The pH values range from negative values to number above 14. Commonly the scale is often misrepresented as ranging from 0 to 14. We will see that negative values are possible.    
Definition of pH, pOH, pKw, pKa, pKb The p" factor" is defined as the log of the whatever quantity that follows the symbol. The "p" is an operator. It communicates the instruction to calculate the negative log of any quantity that follows the symbol. The definition of pH in equation form is 
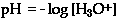
pH = -log[H1+] where [H1+] means the molar concentration of hydronium ions, M = moles / liter This allows the definition of the following series of quantities.
The relationship pH + pOH = 14 In a water solution the ion product for water is: Take the -log of both sides of the equation - log [H+] +(- log [OH- ]) = - log [1 X 10-14 ] pH + pOH = 14 Calculations of pH For strong acids like HCl the molar concentrations are essentially the hydronium ion concentration. These strong acids can produce solutions where the pH can be equal to or less than 1, the pH value would have a value from 0-14. Example: Determination of pH from [H3O+]
Example: Determination of pH from [H3O+] when coefficient is other than "1"
Example: Determination of pH from [OH1- ] using defintion pOH and equation pH + pOH = 14
|
Online Introductory Chemistry
|
|